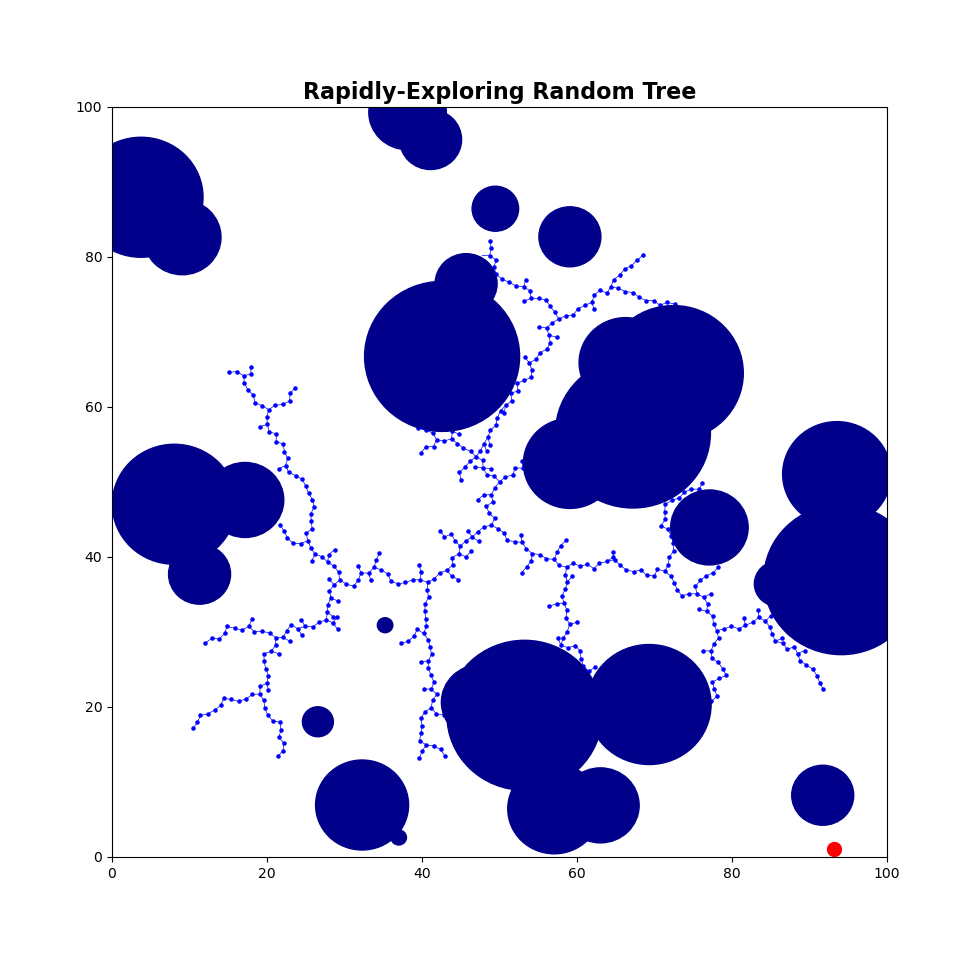
Rapidly-Exploring Random Tree (RRT)
Path Planning, Python, RRT
Overview
Goal: Implement the RRT path-planning algorithm.
GitHub: https://github.com/henryburon/path-planning/tree/main/path_planning
This is an implementation of the Rapidly-Exploring Random Tree (RRT), a fundamental path planning algorithm in robotics.
An RRT consists of a set of vertices, which represent configurations in some domain D and edges, which connect two vertices. The algorithm randomly builds a tree in such a way that, as the number of vertices and n increases to ∞, the vertices are uniformly distributed across the domain D.
In this implementation, the RRT algorithm uses two key components:
- Tree Data Structure: The RRT algorithm maintains a tree data structure to explore and represent the configuration space efficiently. Each node in the tree corresponds to a specific vertex, and edges between nodes represent feasible transitions.
- State Machine: To control the decision-making process during tree expansion and exploration, I employed a state machine to guide the algorithm’s behavior.
The inputs are as follows:
- q_init: initial configuration
- K: max vertices in the RRT
- delta: incremental distance between vertices
- domain: the planning domain (default 100x100)
The algorithm begins by randomly creating the obstacles, initializing the goal (and checking it’s in an acceptable location), and initializing the matplotlib plot. It then begins the main process, which repeats up to K times.
A goal is considered acceptable if it is near the edge of the domain and not inside an obstacle:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
def initialize_goal(self):
acceptable_goal = False
while acceptable_goal == False:
check1 = False
check2 = False
self.x_goal = round(np.random.uniform(self.domain[0],self.domain[1]), 5)
self.y_goal = round(np.random.uniform(self.domain[2],self.domain[3]), 5)
if abs(50 - self.x_goal) > 35 and abs(50 - self.y_goal) > 35: # goal must be near edge of domain (so RRT has to search a little)
check1 = True
for circle in self.circles_list: # goal must not be inside an obstacle
coord = circle["coordinate"]
distance = self.distance(coord, (self.x_goal, self.y_goal))
if distance > circle["size"]:
check2 = True
if check1 and check2:
acceptable_goal = True # proceed with current goal
Every iteration, the algorithm:
- Finds a random configuration (random coordinate within the domain).
- Identifies the closest existing vertex.
- Calculates the direction of the random configuration.
- Plans a new vertex delta (1) in the direction of the random configuration.
-
Checks if the planned vertex collides with an obstacle, and either returns to Step 1 if needed, or continues if there will not be a collision.
Collision checking is implemented as follows:
1 2 3 4 5 6 7 8 9 10
elif self.state == "CHECK_COLLISIONS": for obstacle in self.circles_list: # check each obstacle coord = obstacle["coordinate"] # get center coordinate of obstacle distance = self.distance(coord, self.q_new) if distance < obstacle["size"]: # if new configuration is within obstacle, get new random coordinate self.state = "RANDOM_CONFIG" return else: self.state = "CHECK_FOR_GOAL" # continue to next stage if no collision detected
- Checks if the goal can be spotted (straight line, no obstacles) from the newest vertex. If so, a flag is activated and the algorithm ends.
- Updates the tree with the newest child vertex.
The RRT is then animated with matplotlib.